This post is the summary of Chung, J., Lee, S., & Park, G. (2025). Prediction of high-risk mountain accident areas using a Hurdle model. Korean Journal of Applied Statistics, 38(4), 531-551.

---

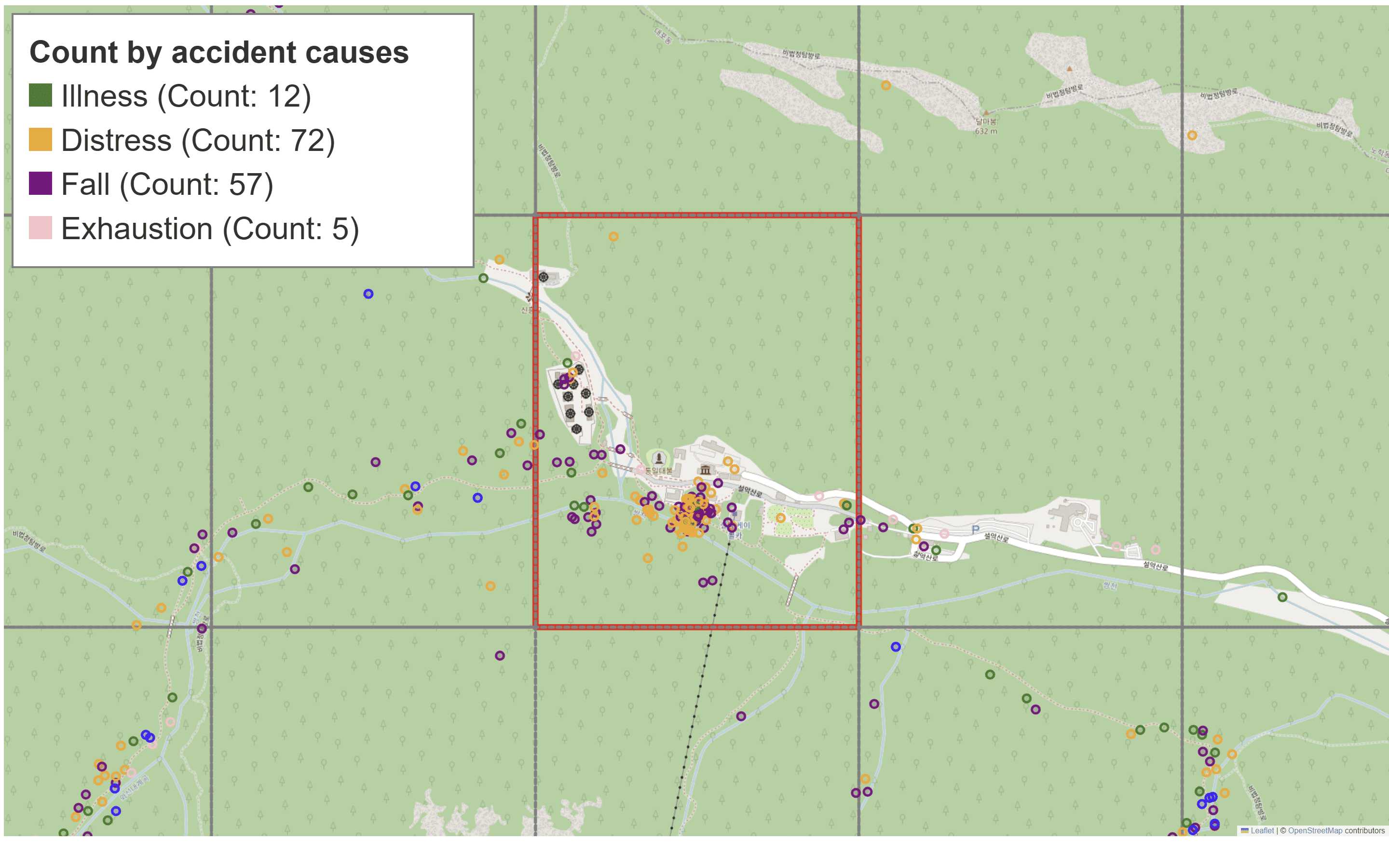
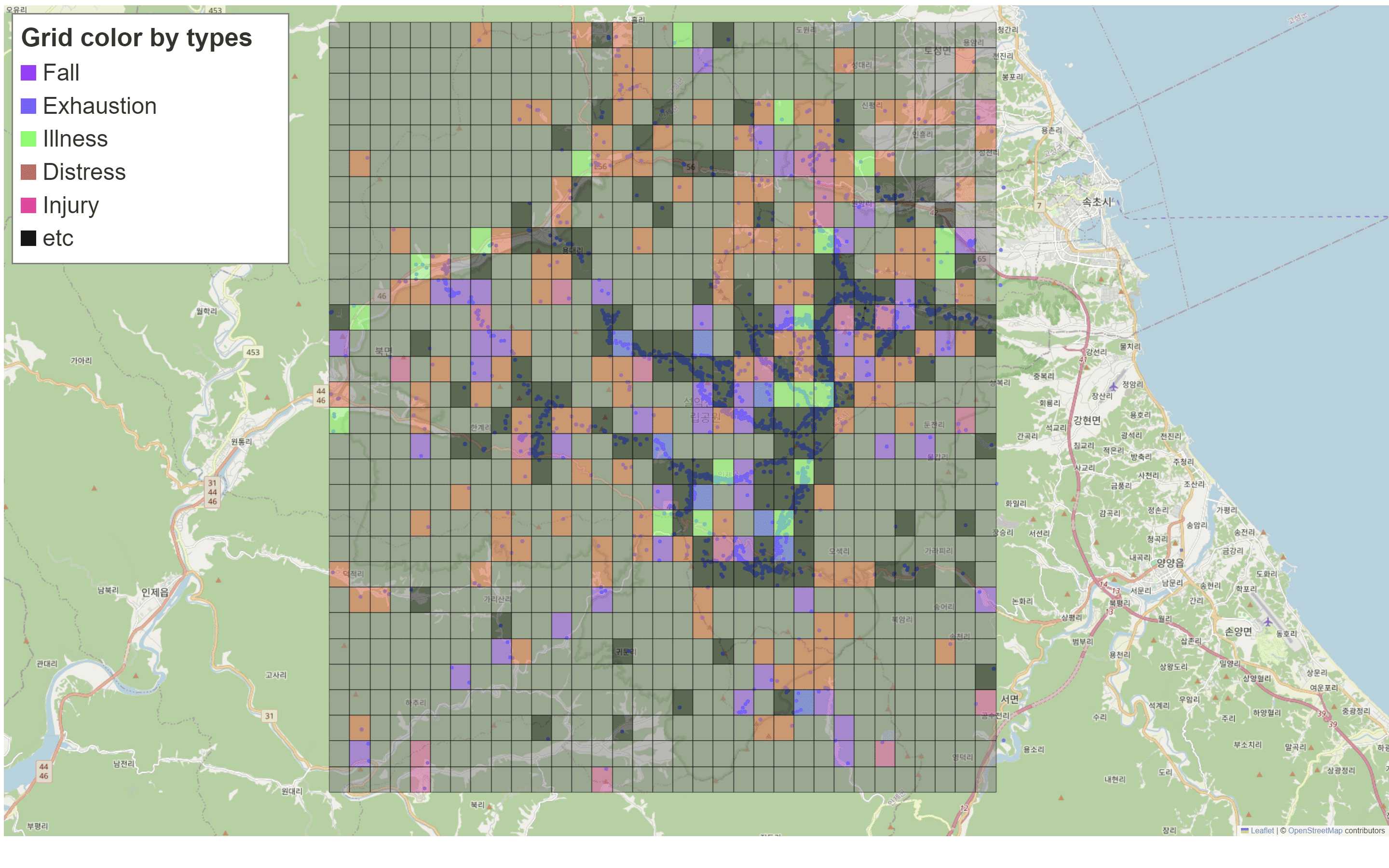
Objective

This study aims to provide a grid-based Hurdle model to predict the average 6-hourly number of mountain accidents using data from 18 mountainous national parks in South Korea.

Contributions

• Applies the grid-based approach, partitioning each national park into a small grid, thereby integrating spatial information such as elevation and slope.
• Uses a Hurdle model to effectively address zero-inflated accident data.
• Reveals that climate-related variables play a crucial role in accident probability, while geological factors (e.g., slope, elevation) are significant for accident frequency.

Hurdle model

• A Hurdle model is a class of statistical models where a random variable is modeled using two parts: (i) the probability to attain zero, and (ii) the probability of the non-zero values.

• Specifically, the $i$-th response variable $Y_i$ follows a Poisson Hurdle model defined as

  \[P(Y_i = y) = \begin{cases} \pi_i , & y = 0, \\ \frac{1-\pi_i}{1-e^{-\lambda_i}} \times \frac{\lambda_i^y e^{-\lambda_i}}{y !} , & y \in \mathbb{N} , \end{cases}\]

  where $\pi_i$ and $\lambda_i$ parameters are modeled by the $i$-th predictor $\mathbf{x}_i$.

• The Poisson Hurdle model is effective as it decouples the zero and non-zero parts, allowing for separate modeling of each process.
• In this study, we apply distinct models for each component:
  • For the zero part: Logistic regression and classification tree-based models (Random Forest, XGBoost, LightGBM, CatBoost).
  • For the non-zero part: Poisson regression and the corresponding regression tree models.

Mountain accident data

Data description

Category	Dataset	Main variables
Input Variables
Terrain	Terrain information	Elevation (m), Slope (°)
Rescue	Accident details	Mountain name, Accident month, Day of the week, Accident time (hour)
Weather	Wind & Pressure	Wind direction/speed (WD, WS), Gust (GST), Atmospheric/Surface pressure (PA, PS), Pressure change (PR, PT)
	Temp & Humidity	Air temperature (TA), Dew point (TD), Humidity (HM), Vapor pressure (PV)
	Precipitation	Rainfall (RN), Daily/Total rainfall, Snow depth (SD), Daily/Total snow depth
	Sky & Visibility	Cloud cover (CA), Cloud height (CH), Visibility (VS), Sunshine (SS), Solar irradiance (SI), Cloud classification (CT)
	Surface & Others	Surface temperature (TS), Soil temperature (TE), Wave height (WH), Weather conditions (WC, WP)
Output Variables
Target	Model Targets	Count: Number of accidents per grid Probability: Accident probability per grid

Accident patterns

Mountain	Area (km²)	Visitors (2023)	\(\hat{P}(Y = 0)\) (No Accident)	\(\hat{P}(Y \geq 1)\) (Accident)	\(\hat{P}(Y \geq 2 \mid Y \geq 1)\) (Multiple)
Jirisan	485.65	2,318,032	0.6151	0.3849	0.5017
Seoraksan	400.03	3,371,633	0.5758	0.4242	0.6288
Sobaeksan	321.26	1,018,623	0.8882	0.1118	0.4614
Odaesan	327.90	1,330,737	0.8946	0.1054	0.4330
Woraksan	288.14	1,680,573	0.8501	0.1499	0.4752

• The above table presents general statistics (area, visitor counts) alongside estimated accident probabilities, where $Y$ denotes the daily number of accidents.
• The proportion of accident-free days ($\hat{P}(Y = 0)$) exceeds 50% for all mountains, highlighting a distinct zero-inflated phenomenon.
• The data suggests a pattern where accidents trigger further accidents ($\hat{P}(Y \geq 2 \mid Y \geq 1)$), as the probability of additional accidents given an occurence is consistently higher than the unconditional accident probability ($\hat{P}(Y \geq 1)$).

Results

Prediction performance

Probability prediction evaluations for each model

Metric	Logistic Regression	Random Forest	XGBoost	LightGBM	CatBoost
Accuracy	0.81	0.81	0.96	0.95	0.93
F1-score	0.27	0.27	0.34	0.47	0.42
BIC	6160.27	5760.58	6272.31	4265.63	4232.00

Count prediction scores by models

Metric	Poisson Regression	Random Forest	XGBoost	LightGBM	CatBoost
MSE	0.24	0.24	0.27	0.26	0.23
Poisson deviance	0.16	0.16	0.17	0.17	0.15
BIC	2439.26	2438.48	2394.82	1720.25	1690.31

• In probability prediction, gradient boosting methods (XGBoost, LightGBM, CatBoost) generally show superior performance compared to linear or tree-based baselines.
  • Specifically, LightGBM achieved the highest F1-score, making it the most suitable model for identifying accident occurrences within imbalanced data.
  • CatBoost recorded the best BIC, demonstrating high efficiency by effectively handling categorical variables with lower dimensionality.
• In count prediction, CatBoost outperforms all other models across every metric.
  • This highlights CatBoost’s strength in leveraging categorical information, which appears crucial for count prediction.
  • Interestingly, other GBDT models did not significantly surpass Poisson Regression, suggesting that the relationship between accident counts and predictors is relatively linear and simple.

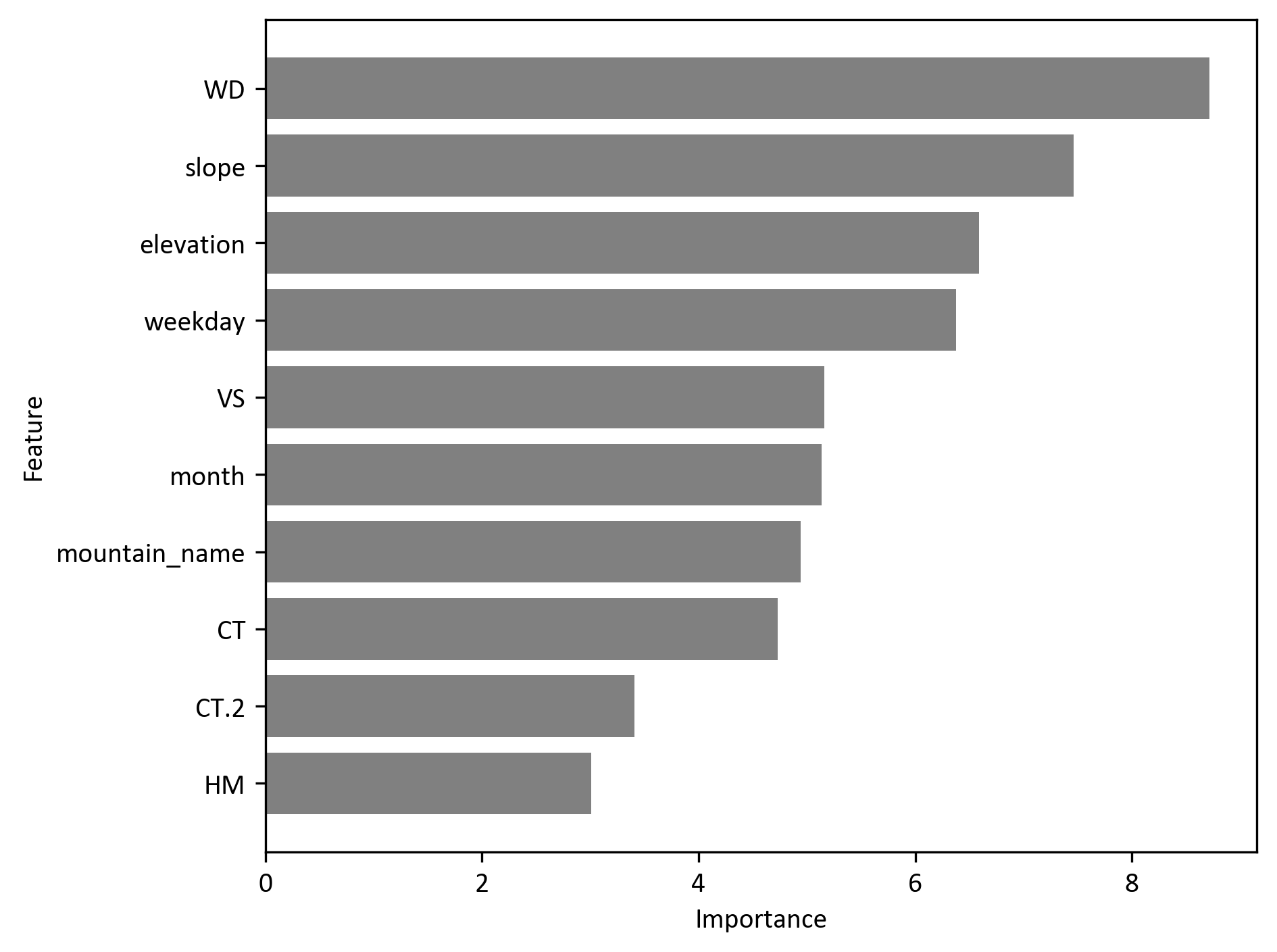
Feature importance analysis

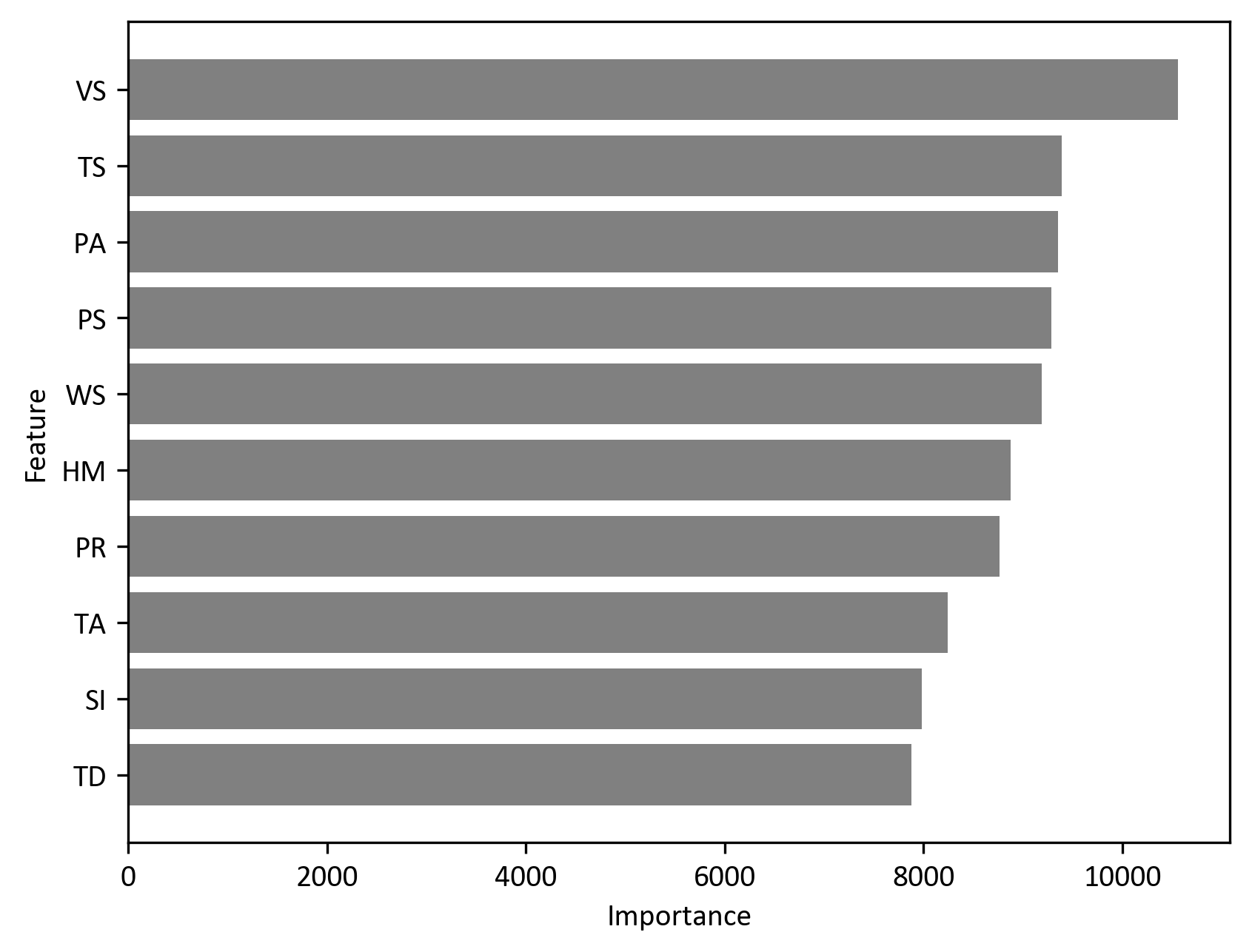
• Probability prediction: Dominantly influenced by weather variables (e.g., visibility, temperature, wind speed), suggesting that immediate meteorological conditions are the primary drivers of accident occurrence.
• Count prediction: Heavily relies on categorical variables (day, month) and terrain features (elevation, slope), indicating that visitor patterns and structural risks drive accident frequency and potential chain reactions.
• Distinct drivers: While visibility and humidity affect both models, terrain factors play a significantly larger role in predicting the number of accidents compared to the mere probability of an event.

References

• Chung, J., Lee, S., & Park, G. (2025). Prediction of high-risk mountain accident areas using a Hurdle model. Korean Journal of Applied Statistics, 38(4), 531-551.