ICA에 관해서 독립 성분 분석 (ICA)에 아주 잘 설명되어 있다고 한번 언급한 적이 있다. 하지만 워낙 흥미롭고 유명한 내용이라 논문을 한번 제대로 훑어보는 것도 좋을 것 같아 리뷰를 하기로 했다. 리뷰할 논문은
A. Hyvärinen, E. Oja의 Indepedent component analysis: algorithms and applications 이다.
1. Motivation
방 안에 있다고 생각해보자. 건너편 방에는 두 사람이 서로 대화하고 있고 그 대화내용은 우리가 있는 방의 스피커를 통해 흘러넘어오고 있다. 시간에 따라 스피커에서 나는 소리를 $x(t)$ 라고 정의해보자. 그렇다면 $x(t)$는 두 명이 각각 내는 소리의 가중합이 될 것이다. 그 두 사람이 내는 소리를 각각 $s_1(t),s_2(t)$라고 표현하면 우리는 아래와 같은 식을 생각할 수 있는 것이다.
\[x(t)=a_1s_1(t)+a_2s_2(t)\]이 때 우리는 과연 $x(t)$만을 가지고 $s_1(t)$과 $s_2(t)$를 분리해낼 수 있을까? 이러한 문제를 칵테일 파티 효과(cocktail-party problem)라고 부른다.
후에 더욱 구체적으로 다루겠지만, 우리가 $s_1(t),s_2(t)$가 동일한 $t$ 하에서 서로 독립이라는 사실만 알고 있어도 $x(t)$를 통해 $s_1(t)$와 $s_2(t)$를 복구해내는 것이 가능하다.
2. Independent component analysis
2.1. Defintion of ICA
$n$개의 independent component로 구성된 $n$개의 linear mixture $x_1,\dots,x_n$을 관측했다고 생각해보자. 즉,
\[x_j = a_{j1}s_1+a_{j2}s_2+\dots+a_{jn}s_n \quad \text{for all } j.\]이는 벡터와 행렬을 통해 더욱 간편하게 표현할 수 있다.
\[\mathbf{x}=\mathbf{As}\] \[\mathbf{x}=\sum_{i=1}^{n} {\mathbf{a}_is_i}\]여기서 핵심은 $s_1,s_2,\dots,s_n$들은 서로 독립인 확률변수라는 점이다. 여기에 우리는 $s_1,s_2,\dots,s_n$들이 non-Gaussian distribution을 따른다는 가정을 추가적으로 하게 되긴 하지만, 이것이 기본 가정은 아니다. 또한 우리는 $\mathbf{A}$를 $n \times n$ 차원 행렬로 정의하고 있는데, 이는 추후에 완회될 수 있는 가정이기도 하다. 다만 이 상태에서 $\mathbf{A}$에 역행렬이 존재한다면
\[\mathbf{s}=\mathbf{A}^{-1}\mathbf{x}\]를 통해 한번에 $\mathbf{s}$를 구할 수 있다는 점에서 장점이 있다.
2.2 Ambiguities of ICA
(3)번 식을 보면 우리는 여기에 몇 가지 모호함이 존재한다는 것을 확인할 수 있다. 이는 마치 Factor Analysis에서의 non-identifiability 문제와 비슷하다.
(i) $\mathbf{s}$의 분산이 특정되지 않는다.
$\mathbf{x}=\mathbf{As}$ 와 $\mathbf{x}=k\mathbf{A}\times\frac{1}{k}\mathbf{s}$ 는 서로 식별되지 않는다. 이는 $\mathbf{s}$의 분산을 하나로 특정할 수 없다는 의미이기도 하다. 이를 해결하기 위해 $E(s_i^2)=1 \; \text{for all }i$ 로 가정을 해준다.
이렇게 해도 $k=-1$일 경우에 대해서는 해결이 되지 않지만 이 경우는 분석에서 크게 문제되지 않는다고 논문에서 말하고 있다.
(ii) independent components의 순서를 알 수 없다.
permutation matrix $\mathbf{P}$에 대해 $\mathbf{x}=\mathbf{AP}^{-1}\mathbf{Ps}$를 해주어도 모형식별이 되지 않는다는 문제점이다. 만약 순서가 중요하다면 문제가 되는 지점이겠지만 그렇지 않을 경우에는 크게 상관이 없다.
2.3. Illustration of ICA
아래의 확률밀도함수를 가지는 확률변수 $S_i(i=1,2)$를 생각해보자.
\[p(s_i) = \begin{cases} \frac{1}{2\sqrt{3}} & \text{if } |s_i| \leq \sqrt{3} \\ 0 & \text{otherwise} \end{cases}\]이 경우 $E(S_i)=0,Var(S_i)=1$이다.
그리고 이 때
\[\mathbf{A} = \left[\begin{matrix} 2 & 3 \\ 2 & 1 \end{matrix}\right]\]의 행렬로 $S_1,S_2$를 섞어보자. 즉,
\[\begin{aligned} &X_1 = 2S_1+3S_2 \\ &X_2 = 2S_1+S_2 \end{aligned}\]으로 $X_1,X_2$라는 새로운 확률변수를 만드는 것이다.

Figure 5는 $S_1,S_2$의 결합분포를 나타내고 있고, Figure 6는 $X_1,X_2$의 결합분포를 나타내고 있다. Figure 6를 보면 마름모 형태의 결합확률분포를 가지는 것을 확인할 수 있는데, $X_1$이 최댓값을 가진다는 사실이 주어진다면 자연스럽게 $X_2$ 역시 최댓값을 가지게 된다. 즉 $X_1,X_2$는 더이상 독립이 아니다.
우리는 $X_1,X_2$만을 관측했을 때 이로부터 $S_1,S_2$를 얻을 수 있는가에 대한 고민을 해야하는 것이다.
3. What is independence?
3.1.과 3.2.에서는 independence에 대한 정의에 대해 다루고 있는데 기초적인 내용이므로 생략하겠다.
3.3. Why Gaussian variables are forbidden
앞서 ICA를 진행하기 위해서는 independence component들이 non-Gaussian distribution을 따른다는 가정이 추가적으로 필요하다는 말이 있었다. 왜 그럴까?
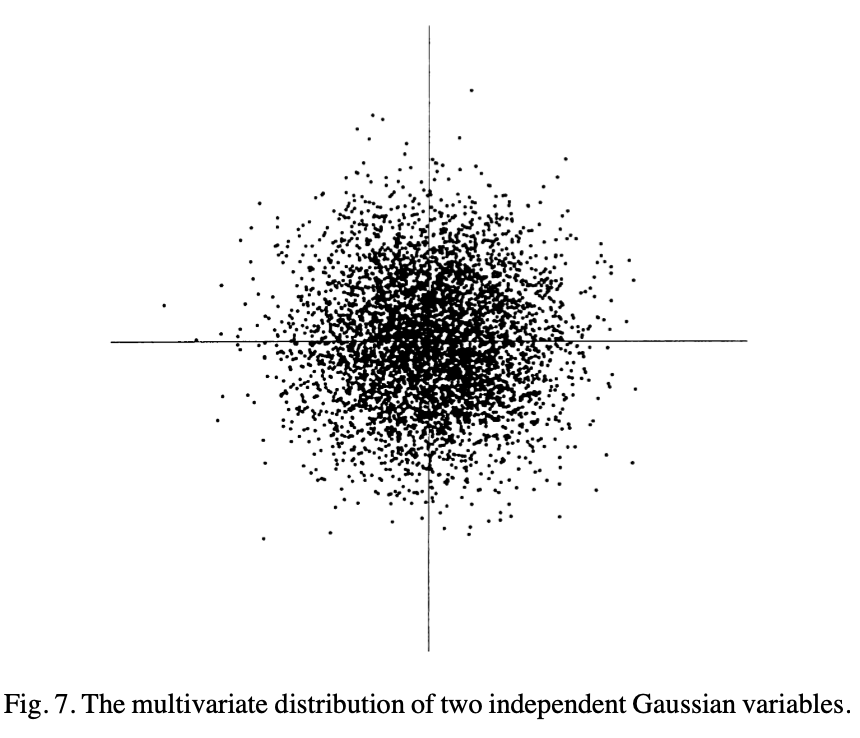
평균이 0이고 분산이 1인 정규분포를 따르며 서로 독립인 두 확률변수의 결합분포를 생각해보자. 2차원상에 표현하면 마치 원의 형태로 나타난다.
이 때 (3)번 식에서의 $\mathbf{A}$가 orthogonal matrix라면, 이 $\mathbf{A}$는 하나로 특정될 수 없다. 결합분포가 원의 형태로 나타나기 때문에 어떻게 회전을 시켜도 설명이 되는 것이다. 그렇기 때문에 모든 확률변수가 Gaussian distribution을 따르는 경우 $\mathbf{A}$를 추정하는 과정에서 non-identifiability 문제가 발생하게 된다.