Research

Statistical structure in complex data

Statistical algorithms for complex data

While modern AI often relies on massive models and large-scale computation, I believe that the essential information in data is fundamentally small and structured. My goal is to design statistical algorithms that identify and utilize this structure, enabling both statistical and computational efficiency.

View my Google Scholar

Optimal transport

Diagram aligning graph-structured source and target spaces through a coupling

Optimal transport has emerged as a fundamental tool in statistics and machine learning for comparing and aligning probability distributions across diverse domains. Beyond its classical formulations, there is an increasing demand for transport methodologies that respect the underlying geometry and structural characteristics of the data spaces. My research focuses on developing geometry-aware and fused optimal transport frameworks that jointly account for domain structure and feature correspondence, enabling principled alignments between heterogeneous spaces.

Key project:

  • Chung, J., Song, E., Kim, W. H., & Park, G. (2026). Convex distance operator transport: A convex and geometry-preserving formulation. Proceedings of the 43rd International Conference on Machine Learning (ICML), PMLR 306, 20900-20940.

Graphical models

Anchored DAG linking latent variables 1–3 to observed variables 1′–3′

Graphical models have long served as a principled framework for uncovering underlying causal structures, benefiting a wide range of fields such as biology, social science, and environmental science. However, data in these domains are often subject to measurement error and other forms of contamination. My research focuses on developing graphical models robust to data contamination, enabling principled and stable learning of dependency structures in complex and imperfect data environments.

Key projects:

  • Shin, J., Chung, J., Hwang, S., & Park, G. (2025). Discovering causal structures in corrupted data: frugality in anchored Gaussian DAG models. Computational Statistics & Data Analysis, 108267.
  • Chung, J., Ahn, Y., Shin, D., & Park, G. (2025). Learning distribution-free anchored linear structural equation models in the presence of measurement error. Journal of the Korean Statistical Society, 54(2), 361-385.

Application

Spatial data

Mountain accident locations by cause with a highlighted grid in Seorak
Seorak grid cells colored by dominant accident type

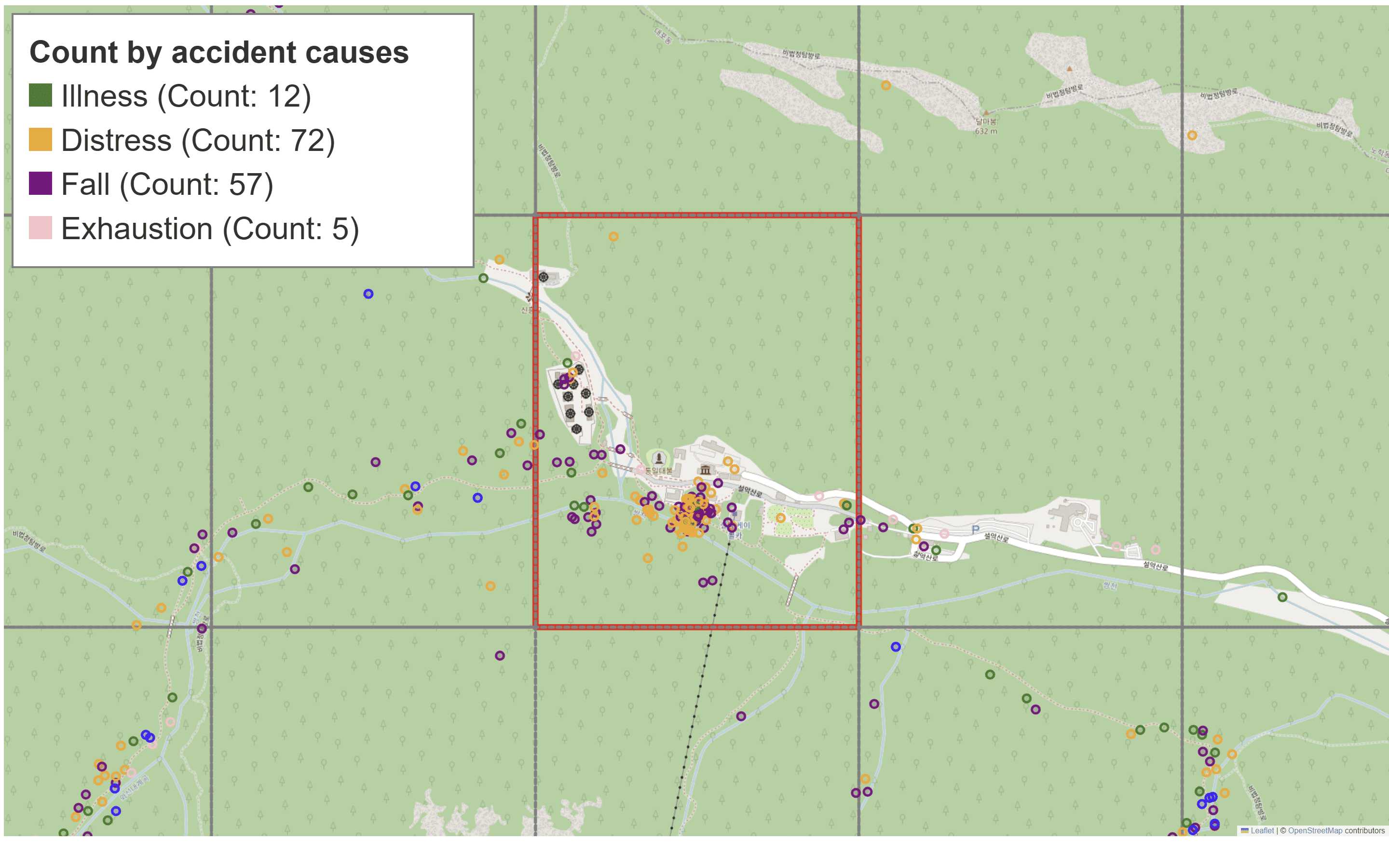
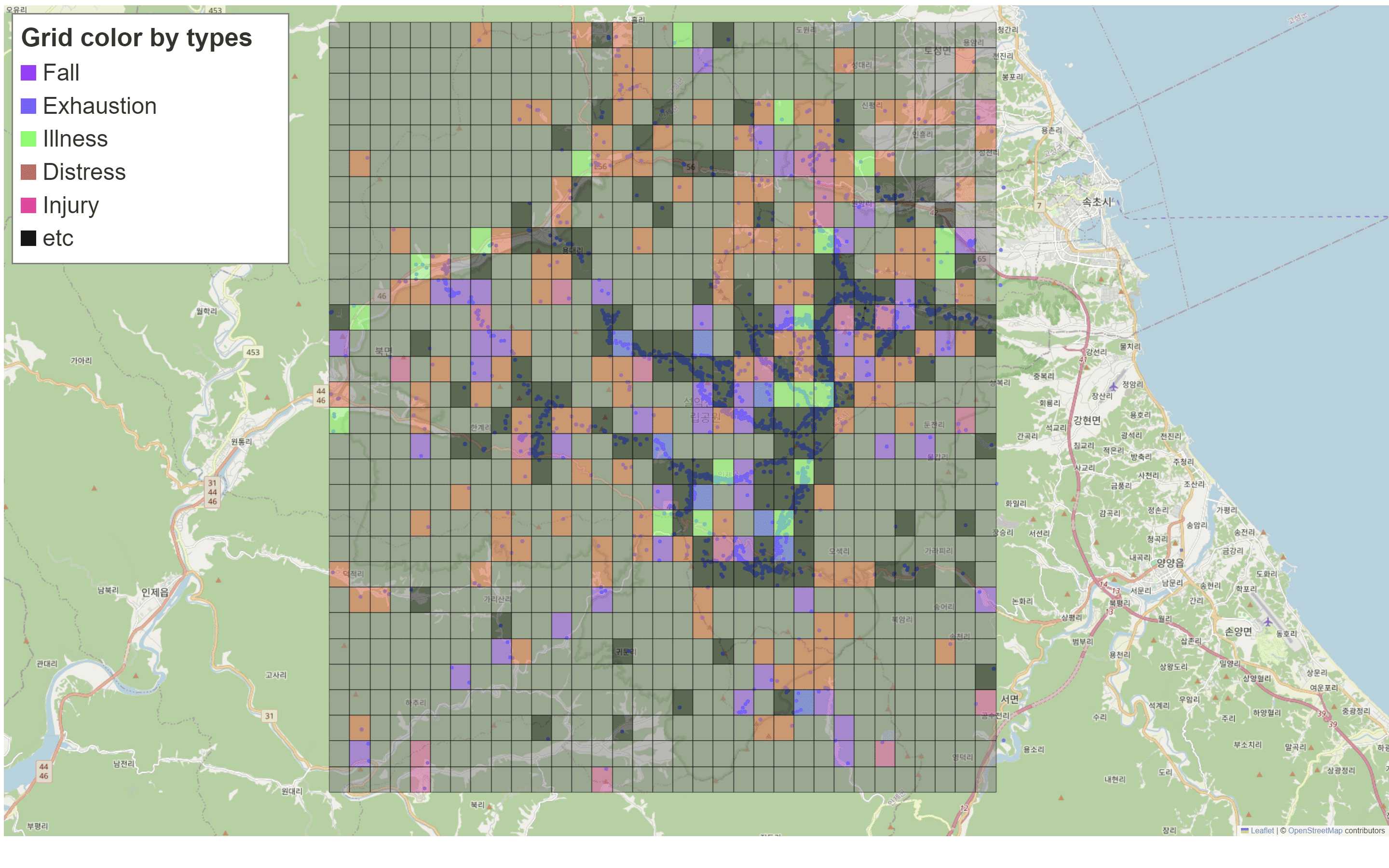
I am interested in spatial data where risk is distributed over complex geographic domains, such as mountain regions with heterogeneous terrain and weather patterns. In one of my projects, I developed statistical models that integrate domain knowledge, covariates, and spatial structure to predict mountain accident risk and identify high risk areas in a transparent and data driven manner.

This line of work has motivated a broader interest in methods that respect underlying spatial geometry, handle sparsity in observations, and provide interpretable output for decision making.

Key project:

  • Chung, J., Lee, S., & Park, G. (2025). Prediction of high-risk mountain accident areas using a Hurdle model. The Korean Journal of Applied Statistics, 38(4), 531-551.

Ranked data

Horse-race ranking illustration with predicted percentages

I am interested in ranked data where the primary object of inference is an ordering rather than a single numeric outcome. In one of my projects, I applied learning-to-rank methods to horse race data, treating each race as a query and each horse as an item. This analysis revealed that pairwise approaches (e.g., LambdaMART) achieve better prediction performance than pointwise approaches (e.g., Random Forest).

This work motivated my broader interest in ranking problems, where samples exhibit strong mutual dependence and must be modeled jointly rather than independently.

Key project:

  • Chung, J., Shin, D., Hwang, S., & Park, G. (2024). Horse race rank prediction using learning-to-rank approaches. The Korean Journal of Applied Statistics, 37(2), 239-253.